Digitaalipiirit/Loogiset operaatiot
Tällä sivulla käsitellään lyhytsanaisesti digitaalitekniikan peruskäsitteitä ennen syvempää perehtymistä digitaalipiireihin.
Boolen Algebra
[muokkaa | muokkaa wikitekstiä]Boolen algebran perusperiaatteeseen kuuluu kaksi arvoa, nämä arvot ovat "tosi" ja "epätosi". Matematiikan helpottamiseksi "tosi" -arvo merkitään luvulla 1 (yksi), ja "epätosi" -arvo merkitään luvulla 0 (nolla). Seuraavaksi näytetään boolen algebran peruslaskutoimitukset:
- yhteenlasku
- 1 + 1 = 1.
- 1 + 0 = 1.
- 0 + 0 = 0.
Huom. Boolen algebrassa on ainoastaan kaksi arvoa (1 ja 0), joten yhteenlaskusta 1 + 1 tulee vastaukseksi 1.
- kertolasku
- 1 * 1 = 1.
- 1 * 0 = 0.
- 0 * 0 = 0.
Komplementointi eli negaatio (EI-operaatio)
[muokkaa | muokkaa wikitekstiä]Tunnetaan myös nimellä Inversio. EI-operaatio kääntää sille annetun arvon, kuten alla olevasta esimerkistä huomaa, tulee ykkösestä nolla, ja toisinpäin nollasta tulee ykkönen. Matemaattisesti EI-operaatiota merkataan "!" (huutomerkki) symbolilla. Esimerkiksi:
- !1 = 0
- !0 = 1
Koska arvot voivat ainoastaan olla joko 1 tai 0, niin on loogista olettaa että jos luku EI ole yksi, niin sitten se on nolla ja jos luku EI ole nolla, niin sitten se on yksi.
Jos kyseessä on muuttuja joka on aina komplementoitu, käytämme seuraavanlaista merkintätapaa:
Jossa X:än yläpuolella oleva viiva ilmaisee muuttujan olevan aina oman arvonsa komplementti.
Looginen yhteenlasku (TAI-operaatio) ja Looginen Kertolasku (JA-operaatio)
[muokkaa | muokkaa wikitekstiä]Matemaattisesti JA portteja käsitellään kertolaskuina ja TAI portteja käsitellään yhteenlaskuina. Muista, Boolen algebrassa yhteenlaskun tulos ei ylitä arvoa 1, vaan 1 + 1 = 1.
JA ja TAI operaatioiden erojen ymmärtämiseksi on hyvä katsoa alla olevaa totuustaulua:
JA/AND TAI/OR
X Y TULOS X Y TULOS 0 0 0 0 0 0 0 1 0 0 1 1 1 0 0 1 0 1 1 1 1 1 1 1
JA operaation tapauksessa kummankin kummankin operandin on oltava 1, jotta tulos olisi 1.
TAI operaation tapauksessa riittää, jos kumpi tahansa operandeista on yksi.
Boolen Algebra
[muokkaa | muokkaa wikitekstiä]Boolen järjestelmässä on kaksi tilaa: Tosi (engl. True) tai Epätosi (engl. False). Näitä tiloja voidaan esittää useilla eri tavoilla, kuten esimerkiksi: on tai off, yksi tai nolla, kyllä tai ei, jne. Näitä tiloja käsitellään kolmella perusoperaatiolla joita kutsutaan loogisiksi operaatioiksi: JA (AND), TAI (OR) ja EI (NOT).
Boolen algebran operaatiot ottavat arvoja vastaan kaksi tai enemmän, ja näillä syötetyillä arvoilla jokainen operaatio antaa odotettavanlaisen ulostulon. Nämä ulostulot on myös kirjoitettu ennalta määrättyihin totuustauluihin. Esimerkiksi JA -operaation ulostulo on aina epätosi, paitsi jos kaikki vastaanotetut arvot ovat tosia.
- Näissä taulukoissa:
- T merkitsee arvoa Tosi ja
- F merkitsee arvoa Epätosi.
- Lukuesimerkki:
- JA-taulukon ensimmäinen rivi ilmaisee että jos A on epätosi ja B on epätosi, niin tulos on epätosi. Saman voi myös ilmaista sanomalla että kun A on 0 ja B on 0, niin tulos on 0, ts. 0 kertaa 0 = 0.
- Taulukon pohjasta näkee, että 1 kertaa 1 on 1.
- TAI-taulukkoa tarkastellessa käytetään plussausta kertomisen sijaan: 0 plus 0 on 0, mutta 0 plus 1 on 1. Samoin 1 plus 1 on 1.
- Kolmas taulukko on EI-taulukko, eli negaatiotaulukko. Negaatiossa arvo kääntyy aina käänteiseksi, eli tosi vaihtuu epätodeksi, ja käänteisessä tapauksessa epätosi vaihtuu todeksi.
|
|
|
On keinoja yhdistää näitä ilmaisuja jotta saadaan aikaiseksi monimutkaisempia ja hyödyllisempiä digitaalipiirejä. Kun käytetään useampaa operaatioita samoille sisääntuloille on mahdollista luoda monimutkaisempia ulostuloja, esimerkiksi näin:
A ja B tai C
Totuustaulu näyttäisi seuraavanlaiselta:
| A | B | C | X |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Tämä totuustaulu noudattaa seuraavanlaisia sääntöjä: Jos A ja B ovat tosia, tai C on tosi, silloin X on tosi
Matemaattiset Operaattorit
[muokkaa | muokkaa wikitekstiä]JA operaatiota esittää symboli tai symboli, missä tapauksessa A JA B näyttäisi tältä tai .
TAI operaatiota esittää symboli tai symboli, missä tapauksessa A TAI B näyttäisi tältä tai .
EI operaatiota esittää symboli tai symboli, missä tapauksessa EI A näyttäisi tältä tai .
Jos operaatioita yhdistelee saadaan aikaiseksi JA-EI (NAND) ja TAI-EI (NOR) operaatiot:
A TAI-EI B (ts. A NOR B) on tai
A JA-EI B (ts. A NAND B) on tai
Boolen Algebran Säännöt
[muokkaa | muokkaa wikitekstiä]Boolen Algebrassa, kuten tavallisessakin algebrassa, on tiettyjä sääntöjä. Nämä säännöt ovat Liitännäisyys eli assosiatiivisuus, Osittelulaki eli distributiivisuus, Kommutatiivisuus eli vaihdannaisuus ja De Morganin Laki. Assosiatiivisuus, distributiivisuus ja vaihdannaisuus koskevat ainoastaan JA ja TAI operaatioita.
Liitännäisyys eli assosiatiivisuus
[muokkaa | muokkaa wikitekstiä]Liitäntä- eli assosiatiivisuuslain mukaan muuttujat voidaan ryhmitellä vapaasti TAI-operaatiossa ja JA-operaatiossa.
Tai
Osittelulaki eli distributiivisuus
[muokkaa | muokkaa wikitekstiä]Osittelu- eli distributiivisuuslain mukaan määritellän yhteisen yhteenlaskettavan ja yhteisen tekijän ottaminen.
Tai
Kommutatiivisuus eli vaihdannaisuus
[muokkaa | muokkaa wikitekstiä]Vaihdantalaki tarkoittaa sitä, että muuttujien järjestyksellä TAI-operaatiossa ja JA-operaatiossa ei ole merkitystä.
Tai
De Morganin Laki
[muokkaa | muokkaa wikitekstiä]De Morganin kaavat ovat välttämättömiä komplementteja sisältävien lausekkeiden sievennyksessä. Kaavoissa muuttujien lukumäärää ei ole rajoitettu. Kaavojen mukaan lausekkeen päällä olevan komplementtiviiva voidaan jakaa muuttujien päälle, jos samalla muuttujien välinen operaatio vaihdetaan. De Morgan's Law is a consequence of the fact that the not or negation operator is not distributive.
Tai
Huomautukset
[muokkaa | muokkaa wikitekstiä]On tärkeää huomata että
- tai
Tämä voidaan nähdä joko JA operaationa jolla on korkeampi etusija, tai että assosiatiivisuus ei koske JA ja TAI operaatioiden välillä, tai että se on pätemätön käyttö distributiivisuudelle.
Säännöt
[muokkaa | muokkaa wikitekstiä]Näiden lakien seurauksena tulee joitakin sääntöjä, joita noudatetaan Boolen Algebrassa.
Tai vaihtoehtoista merkintätapaa käyttäen
Tuplanegaatio:
Duaalisuusperiaate
[muokkaa | muokkaa wikitekstiä]Dualisuusperiaatteen mukaan: Jos boolen yhtälössä vaihdamme 'JA' ja 'TAI' operaattorien paikkaa, sekä vaihdamme '0' ja '1' arvojen paikkoja, boolen yhtälön tulos on edelleen oikein.
Esimerkiksi: Jos olemme tietoisia siitä että A·(B+C)=A·B+A·C tuolloin
Vasemman puolen duaali on A+B·C
Oikean puolen duaali on (A+B)·(A+C)
Duaalisuusperiaatteen mukaan voimme sanoa että A+B·C=(A+B)·(A+C)
Esimerkkejä
[muokkaa | muokkaa wikitekstiä]Yksinkertaista seuraavat ilmaisut.
Tai
Ykköstä varten käytämme sääntöä nro 7. Tästä saamme.
- tai
Mikä sattuu olemaan sääntö 5, joten vastaus on nolla. Kakkosessa voimme ottaa pois A:n. Tästä saamme
- tai
Aaltosulkeet ovat sääntö nro 8. Joten vastaus on A.
Katso myös
[muokkaa | muokkaa wikitekstiä]Mikä on Totuustaulu?
[muokkaa | muokkaa wikitekstiä]Kytkentäfunktio voidaan määritellä täydellisesti, paitsi kytkentäalgebran lausekkeella, myös taulukkona eli totuustauluna (truth table). Totuustaulussa esitetään piirin toteuttaman funktion arvo kaikilla mahdollisilla muuttujien arvojen kombinaatioilla. Koska muuttujalla on vain kaksi erilaista arvoa, niin erilaisten arvojen kombinaatioiden lukumäärä on 2n, jossa n on piirin muuttujien lukumäärä.
Loogisten perusoperaatioiden totuustaulut
[muokkaa | muokkaa wikitekstiä]Käytämme seuraavaa diagrammia totuustaulujen kirjoittamiseen:
A ---+--------+
| Portti |-----Y
B ---+--------+
Missä A ja B ovat sisääntulot kyseiselle portille, ja Y on ulostulo kyseiseltä portilta. Yleisimmät loogiset portit ovat JA, TAI, EHDOTON-TAI, JA-EI ja invertoitu EHDOTON TAI.
AND (JA-operaatio)
[muokkaa | muokkaa wikitekstiä]

JA portilla on seuraavanlainen totuustaulu:
- Sekä A JA B pitävät olla TOSIA jotta ulostulo Y voisi olla tosi
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR (TAI-operaatio)
[muokkaa | muokkaa wikitekstiä]

TAI portilla on seuraavanlainen totuustaulu:
- Joko A TAI B TAI MOLEMMAT pitää olla TOSI, jotta ulostulo Y olisi tosi
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR (EHDOTON TAI-operaatio)
[muokkaa | muokkaa wikitekstiä]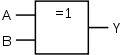

EHDOTON TAI portilla on seuraavanlainen totuustaulu:
- Jompikumpi A TAI B (mutta vain toinen) pitää olla tosi, jotta ulostulo Y olisi tosi
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NAND (invertoitu JA-operaatio)
[muokkaa | muokkaa wikitekstiä]
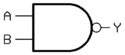
Invertoitu JA portilla on seuraavanlainen totuustaulu:
- Yksinkertaisesti "EI JA"
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR (invertoitu TAI-operaatio)
[muokkaa | muokkaa wikitekstiä]

Invertoitu TAI portilla on seuraavanlainen totuustaulu:
- Yksinkertaisesti "EI TAI"
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR (invertoitu EHDOTON TAI-operaatio)
[muokkaa | muokkaa wikitekstiä]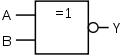

Invertoitu EHDOTON TAI portilla on seuraavanlainen totuustaulu:
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

































































